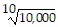Prove 
for all natural numbers n.
?
List the steps involved.
What will be an ideal response?
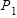is true. However, 
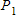is just the statement that 
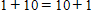, which is true.Step 2: Assuming that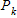 
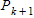
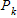
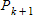
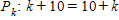
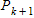
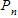
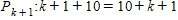
is true, we must prove that 
is true. Let's examine 
and 
.
.
is obtained by substituting k+1 for n in 
.
.
If we add 1 to the both sides of the equation for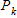 
, we'll get the equation for 
.
Since equation for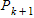 
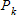
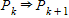
follows from equation for 
, we have demonstrated that 
.
?
You might also like to view...
Find the derivative of the function by using the definition.y =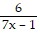 
A. - 
B. -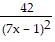 
C. - 
D.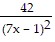 
Find the exact value of the expression.cos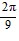 
sin 
- cos 
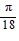sin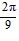 
A.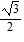 
B. 
C.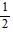 
D. 1
Find the center and radius of the circle.x2 + y2 = 64
A. Center: (0, 0); radius: 64 B. Center: (1, 1); radius: 64 C. Center: (1, 1); radius: 8 D. Center: (0, 0); radius: 8
Simplify the expression. Assume that all variables are positive and write your answer in radical notation.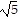
? 
A.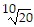 
B.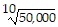 
C.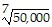 
D. 