Solve the problem.A projectile is fired from a cliff 300 feet above the water at an inclination of 45° to the horizontal, with a muzzle velocity of 300 feet per second. The height h of the projectile above the water is given by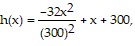 
where x is the horizontal distance of the projectile from the base of the cliff. How far from the base of the cliff is the height of the projectile a maximum?
A. 703.13 ft
B. 1,003.13 ft
C. 2,409.38 ft
D. 1,406.25 ft
Answer: D
You might also like to view...
Find the derivative of the function.y = log (6x)
A. 
B. 
C.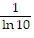 
D. 
Find the Taylor polynomial of order 3 generated by f at a.f(x) = x2 + x + 1, a = 6
A. P3(x) = 7 + 13(x - 6) + 19(x - 6)2 B. P3(x) = 43 + 13(x - 6) + 13(x - 6)2 + 43(x - 6)3 C. P3(x) = 43 + 13(x - 6) + (x - 6)2 D. P3(x) = 1 + 3(x - 6) + 3(x - 6)2 + (x - 6)3
Use elimination to solve each system of equations, if possible. Identify the system as consistent or inconsistent. If the system is consistent, state whether the equations are dependent or independent.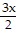 
- 
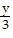= -18
+ 
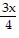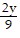= -9
A. (-12, 0); consistent and independent B. (0, -12); consistent and independent C. (0, 12); consistent and independent D. (12, 0); consistent and independent
Graph the function. Give the domain and range.f(x) =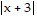 
A. Domain: (-?, ?); Range: [0, ?)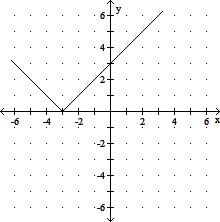
B. Domain: (-?, ?); Range: [- 3, ?)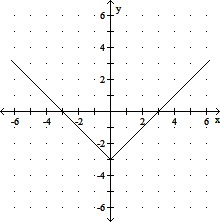
C. Domain: (-?, ?); Range: [0, ?)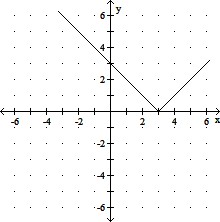
D. Domain: (-?, ?); Range: [3, ?)