Graph the function, then find the extreme values of the function on the interval and indicate where they occur.y =  -
- 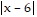 on the interval -2 < x < 7
on the interval -2 < x < 7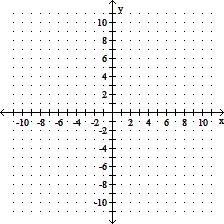
A. Absolute maximum is 4
on the interval [6, 7);
Absolute minimum is -3
on the interval (-2, 3]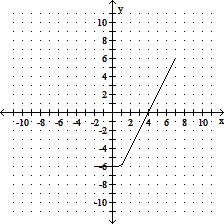
B. Absolute maximum is -4
on the interval [6, 7);
Absolute minimum is 4
on the interval (-2, 2]
C. Absolute maximum is 5
on the interval [6, 7);
Absolute minimum is -3
on the interval (-2, 2]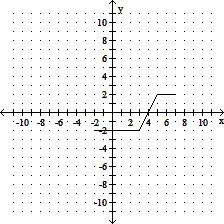
D. Absolute maximum is 4
on the interval [6, 7);
Absolute minimum is -4
on the interval (-2, 2]
Answer: D
You might also like to view...
Solve the problem.How many different three-number "combinations" are possible on a combination lock having 22 numbers on its dial? Assume that no numbers repeat. (Combination locks are really permutation locks.)
A. 9240 B. 351,120 C. 1,053,400 D. 175,560
Match the quadratic function to the correct graph.y = -(x + 4)2 + 3
A. 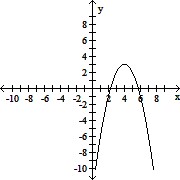
B. 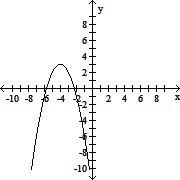
C. 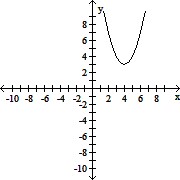
D. 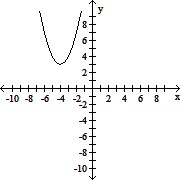
Perform the operation and write the result in the standard form.7i(5 - 5i)
A. 35i + 35i2 B. 35i - 35 C. 35 + 35i D. - 35i - 35i2
Evaluate the expression ![]() .
.
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. ![]()