The given situation involves a rate of change that you may assume to be constant. Write a statement that describes how one variable varies with respect to another, give the rate of change numerically (with units), and use the rate of change rule to answer the questions.You drive along the highway at a constant speed of 62 miles per hour. How far do you travel in 4.1 hours? In 6.3 hours? Write a statement that describes how one variable varies with respect to another.
A. Your distance traveled changes with respect to time at a rate of 62 miles per hour. The rate of change is 62 mi/hr. In 4.1 hours, you travel 254.2 miles. In 6.3 hours, you travel 390.6 miles.
B. Your distance traveled changes with respect to time at a rate of 62 miles per hour. The rate of change is 62 mi/hr. In 4.1 hours, you travel 127.1 miles. In 6.3 hours, you travel 195.3 miles.
C. Your distance traveled changes with respect to time at a rate of 62 miles per hour. The rate of change is 62 mi/hr. In 4.1 hours, you travel 190.65 miles. In 6.3 hours, you travel 292.95 miles.
D. Your distance traveled changes with respect to time at a rate of 62 miles per hour. The rate of change is 62 mi/hr. In 4.1 hours, you travel 317.75 miles. In 6.3 hours, you travel 488.25 miles.
Answer: A
You might also like to view...
Using complements (with respect to 1) of the single discounts, find the net cost equivalent for the following discount.25/25/25/5
A. 0.4 B. 0.6 C. 0.40078125 D. 0.59921875
Complete the sketch so that it has the indicated symmetry.Complete the sketch so that it has 45° rotational symmetry about O.![]()
What will be an ideal response?
Solve the problem.Tom Quig traveled 260 miles east of St. Louis. For most of the trip he averaged 60 mph, but for one period of time he was slowed to 20 mph due to a major accident. If the total time of travel was 7 hours, how many miles did he drive at the reduced speed?
A. 75 miles B. 90 miles C. 80 miles D. 100 miles
Find an equation of the line.Parallel to y = -12, through (5, -6)
A. y = -6
B. y = 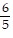 x - 12
x - 12
C. y = 5
D. x = 5