Solve the problem.The approximate rate of change in height of a certain shrub in a nursery is given by 
where the height is measured in inches and x represents the number of years since the shrub was planted. After 2 years, the shrub was 19 inches tall. Find the function that gives the height of the shrub x years after it was planted. Assuming that the shrub will be sold when it is 7 years old, approximate its height when it is sold.
A. f(x) = 14 ln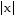
+ 9.3; 36.5 inches
B. f(x) = 14 ln
+ 19; 46.2 inches
C. f(x) =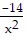 
+ 
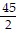; 22.2 inches
D. f(x) = 14 ln
+ 19; 41.5 inches
Answer: A
You might also like to view...
Solve the problem.The strength S of a rectangular wooden beam is proportional to its width times the square of its depth. Find the dimensions of the strongest beam that can be cut from a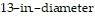 
cylindrical log. (Round answers to the nearest tenth.)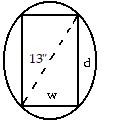
A. w = 7.5; d = 10.6 B. w = 8.5; d = 9.6 C. w = 8.5; d = 11.6 D. w = 6.5; d = 11.6
Use the compound interest formula to determine the final value of the given amount.$1,000 at 5% compounded annually for 4 years
A. $1157.63 B. $1215.51 C. $215.51 D. $1276.28
Complete.42.8 dm = 
m
A. 4.28 B. 428 C. 4,280 D. 0.428
In the table, Y1 is defined as a quadratic function. Use the table to do the following: a. Determine the coordinates of the vertex of the graph. b. Determine whether the vertex is a minimum point or a maximum point. c. Find the minimum or maximum value of the function. d. Determine the range of the function.
A. a. (7, -3); b. minimum; c. -3; d. [-3, ?) B. a. (-3, 7); b. minimum; c. 7; d. [7, ?) C. a. (7, -3); b. maximum; c. -3; d. (-?, -3] D. a. (-3, 7); b. maximum; c. 7; d. (-?, 7]