Find the limit.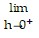
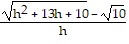
A. Does not exist
B.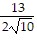 
C.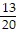 
D.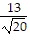 
Answer: B
You might also like to view...
Find the maximum and minimum of the function f over the closed and bounded set S.f(x, y) = (x + y)2; S = {(x, y):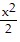 
+ 
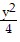? 1}
A. f(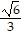
, 
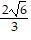) = f(- 
, - 
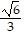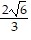) = 6; maximum. f(x, -x) = 0 for - 
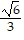? x ? - 
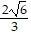; minimum.
B. f(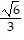
, 
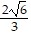) = f(- 
, - 
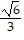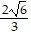) = 6; maximum. f(x, -x) = 0 for - 
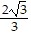? x ?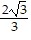 
; minimum.
C. f(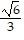
, 
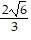) = 6; maximum. f(- 
, - 
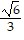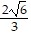) = 6; minimum.
D. f(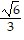
, 
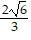) = 6; maximum. f(- 
, - 
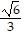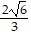) = -6; minimum.
Solve the problem.About how accurately must the interior diameter of a cylindrical storage tank that is 12 m high be measured in order to calculate the tank's volume within 2% of its true value?
A. Within 2% B. Within 1% C. Within 2 meters D. Within 1 meters
Solve the linear equation.5x + 5 = 6(x + 4)
A. 29 B. -29 C. -19 D. 19
Solve the problem.A store makes two different types of smoothies by blending different fruit juices. Each bottle of Orange Daze smoothie contains 10 fluid ounces of orange juice, 4 fluid ounces of pineapple juice, and 2 fluid ounces of blueberry juice. Each bottle of Pineapple Blue smoothie contains 5 fluid ounces of orange juice, 6 fluid ounces of pineapple juice, and 4 fluid ounces of blueberry juice. The store has 500 fluid ounces of orange juice, 360 fluid ounces of pineapple juice, and 250 fluid ounces of blueberry juice available to put into its smoothies. The store makes a profit of $1.50 on each bottle of Orange Daze and $1 on each bottle of Pineapple Blue. How many bottles of each smoothie should the store make to maximize its profit? What is the maximum profit?
A. Maximum profit is $80 when the store makes 40 bottles of Orange Daze and 20 bottles of Pineapple Blue. B. Maximum profit is $85 when the store makes 30 bottles of Orange Daze and 40 bottles of Pineapple Blue. C. Maximum profit is $75 when the store makes 50 bottles of Orange Daze and 0 bottles of Pineapple Blue. D. Maximum profit is $87.50 when the store makes 35 bottles of Orange Daze and 35 bottles of Pineapple Blue.