Solve the problem.The equation y = 0.002x - 0.20 can be used to determine the approximate profit, y in dollars, of producing x items. How many items must be produced so the profit will be at least $3933?
A. x ? 1,966,600
B. x ? 1,966,400
C. x ? 1,966,600
D. 0 < x ? 1,966,599
Answer: C
You might also like to view...
Identify equilibrium values and determine which are stable and which are unstable.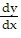
= (y + 2)(y + 1)
A. y = 2 is a stable equilibrium value and y = 1 is an unstable equilibrium. B. y = 1 is a stable equilibrium value and y = -2 is an unstable equilibrium. C. y = -2 is a stable equilibrium value and y = 1 is an unstable equilibrium. D. y = -1 is a stable equilibrium value and y = 2 is an unstable equilibrium.
Convert as indicated.30,000 pounds to tons
A. 16 tons
B. 15 tons
C. 14 tons
D. 15
tons
Solve the problem.Since the end of the Cold War, jobs in defense manufacturing and aerospace have disappeared as the U.S. government spends less on defense. Employments at Aerospace Tech for various years are listed in the table below.
Let L represent the employment (in thousands of people) at Aerospace Tech t years since 1922.i) Use your graphing calculator to create a scatterplot of the Aerospace Tech data. Then use your calculator to sketch the graph of the equation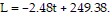 
Which data point(s) are above the line?ii) Use the linear model to estimate when there were 35
thousand employees at Aerospace Tech.iii) Use the linear model to predict the number of employees at Aerospace Tech in 2032. Has model breakdown occurred?iv) What is the slope of the equation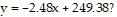 
What does the slope tell you in terms of the employment at Aerospace Tech - be as specific and complete as you can be.v) Find the t-intercept. What does your result mean in terms of Aerospace Tech?vi) Find the L-intercept. What does your result mean in terms of Aerospace Tech?
What will be an ideal response?
Evaluate the expression for othe given values of the variables.x2 + 3x + 1 for x = 6
A. 40 B. 25 C. 31 D. 55