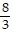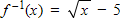Restrict the domain of the function f so that the function is one-to-one and has an inverse function. Then find the inverse function f-1. State the domains and ranges of f and f-1.
?
f(x) = (x - 5)2
?
A. 
?
The domain of f and the range of f-1 are all real numbers x such that x ? 5.
The domain of f-1 and the range of f are all real numbers x such that x ? 0.
B.
?
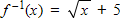
The domain of f and the range of f-1 are all real numbers x such that x ? 0.
The domain of f-1 and the range of f are all real numbers x such that x ? -5.
C.
?
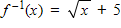
The domain of f and the range of f-1 are all real numbers x such that x ? 5.
The domain of f-1 and the range of f are all real numbers x such that x ? 0.
D.
?
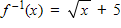
The domain of f and the range of f-1 are all real numbers x such that x ? 0.
The domain off-1 and the range offare all real numbersxsuch thatx ? 5.
E.
?
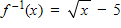
The domain of f and the range of f-1 are all real numbers x such that x ? -5.
The domain of f-1 and the range of f are all real numbers x such that x ? 0.
Answer: C
You might also like to view...
Find the value of the combination.C(6, 4)
A. 30 B. 15 C. 180 D. 4
An arithmetic sequence is given. Find the common difference and write out the first four terms.{11 - 6n}
A. d = 6; 5, 11 , 17 , 23 B. d = -6; 5, 1 , -5 , -11 C. d = -6; 5, -1, -7, -13 D. d = -6; -6, -12, -18, -24
Fill in the blank with one of the words or phrases listed below.
The 
method may be used when multiplying two binomials.
A. term B. coefficient C. FOIL D. degree of a term
Solve the problem.Suppose the supply function of a certain item is given by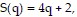 
and the demand function is given by D(q) = 14 - q2. Find the producers' surplus.
A. 16
B. 8
C.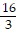 
D. 