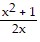Solve the problem.A lumber yard has fixed costs of $3637.50 a day and variable costs of $1.00 per board-foot produced. The company gets $2.50 per board-foot sold. How many board-feet must be produced daily to break even?
A. 1039 board-feet
B. 1616 board-feet
C. 3637 board-feet
D. 2425 board-feet
Answer: D
You might also like to view...
Determine whether the graph is the graph of a function.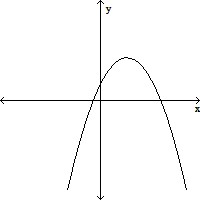
A. Function B. Not a function
Use the Runge-Kutta method to find y-values of the solution for the given values of x and ?x, if the curve of the solution passes through the given point.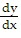
= x + sin y; x = 0 to 0.3; ?x = 0.1; (0, 1)
A.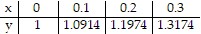 
B. 
C. 
D. 
Solve the problem.The inequality |T - 35| ? 18 describes the range of monthly average temperatures T in degrees Fahrenheit at a City X. (i) Solve the inequality. (ii) If the high and low monthly average temperatures satisfy equality, interpret the inequality.
A. 14 ? T ? 56; The monthly averages are always within 
B. T ? 53; The monthly averages are always less than or equal to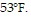 
C. 17 ? T ? 53; The monthly averages are always within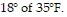 
D. 14 ? T; The monthly averages are always greater than or equal to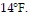 
Perform the indicated operations and simplify the result. Leave the answer in factored form.
A. 1
B. 
C. 
D. 