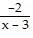Solve the differential equation subject to the initial conditions.t
+ 4y = t3; t > 0, y = 1 when t = 2
A. y =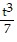 
+ 
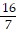t-4, t > 0
B. y =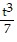 
+ 
t-4, t > 0
C. y =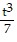 
- 
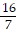t-4, t > 0
D. y =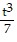 
- 2t-4, t > 0
Answer: C
You might also like to view...
The graph of the polynomial f(x) is shown in the figure. Estimate the zeros and state whether their multiplicities are odd or even.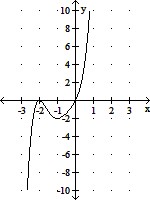
A. -2 (odd), 0 (odd) B. -2 (even), 0 (odd) C. -2 (even), 0 (even) D. -2 (odd), 0 (even)
Answer the question.How can the graph of f(x) = -(x - 10)2 + 4 be obtained from the graph of y = x2?
A. Shift it horizontally 10 units to the left. Reflect it across the 
Shift it 4 units up.
B. Shift it horizontally 10 units to the right. Reflect it across the 
Shift it 4 units up.
C. Shift it horizontally 10 units to the right. Reflect it across the 
Shift it 4 units up.
D. Shift it horizontally 10 units to the right. Reflect it across the 
Shift it 4 units down.
Graph the solution set on a number line.{x|-4 < x < 0}
A. 
B. 
C. 
D. 
Write the partial fraction decomposition of the rational expression.
A.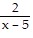 
+ 
B. 
+ 
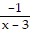
C.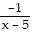 
+ 
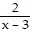
D.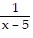 
+ 