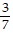Find the vertex form for the quadratic function. Then find each of the following:(A) Intercepts(B) Vertex(C) Maximum or minimum(D) Rangem(x) = -x2 - 8x - 7
A. Standard form: m(x) = -(x + 4)2 + 9
(A) x-intercepts: - 7, -1; y-intercept: -7
(B) Vertex (4, -9)
(C) Maximum: 9
(D) y ? 9
B. Standard form: m(x) = -(x - 4)2 + 9
(A) x-intercepts: - 7, -1; y-intercept: -7
(B) Vertex (-4, 9)
(C) Minimum: 9
(D) y ? 9
C. Standard form: m(x) = -(x - 4)2 + 9
(A) x-intercepts: 1, 7; y-intercept: -7
(B) Vertex (-4, 9)
(C) Maximum: 9
(D) y ? 9
D. Standard form: m(x) = -(x + 4)2 + 9
(A) x-intercepts: - 7, -1; y-intercept: -7
(B) Vertex (-4, 9)
(C) Maximum: 9
(D) y ? 9
Answer: D
You might also like to view...
Provide an appropriate response.A daily round trip train ticket to the city costs $4.25. Let x represent the passenger's income and y represent the cost of a daily round trip train ticket. Write an equation which represents the relationship between the cost of a daily round trip ticket and a passenger's income; describe the graph of this equation, and identify the intercepts.
What will be an ideal response?
Without using a calculator, give the exact trigonometric function value with rational denominator.sec 45°
A.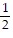 
B. 1
C.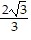 
D.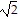 
Find the center, transverse axis, vertices, and foci of the hyperbola.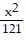
- 
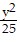= 1
A. center at (0, 0)
transverse axis is x-axis
vertices at (-5, 0) and (5, 0)
foci at (-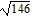 
, 0) and (
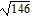, 0)
B. center at (0, 0)
transverse axis is x-axis
vertices at (-11, 0) and (11, 0)
foci at (-5, 0) and (5, 0)
C. center at (0, 0)
transverse axis is y-axis
vertices at (0, -11) and (0, 11)
foci at (-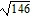 
, 0) and (
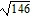, 0)
D. center at (0, 0)
transverse axis is x-axis
vertices at (-11, 0) and (11, 0)
foci at (-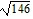 
, 0) and (
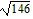, 0)
Simplify completely. If the fraction is improper, write it as a mixed number.
A.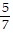 
B. 
C.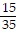 
D. 