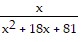Use the frequency distribution to find the mean and the sample standard deviation. Does the data form a normal distribution? Remember: if the data fall within 2% of the empirical rule of 68%, 95%, and 99.7% for one, two, or three standard deviations, respectively, they form a normal distribution.
Life of bulb (hours) Frequencyf0 - 999.5 103999.5 - 1,999.5 4761,999.5 - 2,999.5 2,0622,999.5 - 3,999.5 4,1293,999.5 - 4,999.5 2,4604,999.5 - 5,999.5 4215,999.5 - 6,999.5 146
A. The mean is 3,546 hours. The sample standard deviation is 1,018 hours. The data forms a normal distribution.
B. The mean is 3,523 hours. The sample standard deviation is 1,017 hours. The data forms a normal distribution.
C. The mean is 3,546 hours. The sample standard deviation is 1,018 hours. The data doesn't form a normal distribution.
D. The mean is 3,542 hours. The sample standard deviation is 1,027 hours. The data forms a normal distribution.
E. The mean is 3,523 hours. The sample standard deviation is 1,017 hours. The data doesn't form a normal distribution.
Answer: D
You might also like to view...
Find the limit.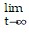
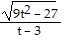
A. 9 B. 27 C. 3 D. Does not exist
Solve the equation.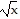 + 1 =
+ 1 = 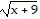
A. x = 16 B. x = 4 C. no solution D. x = 64
Solve the problem. If necessary, round to the nearest tenth, unless intructed otherwise.Tickets for a play are sold at two prices; $18, and $30. Find a formula for the total cost T (in dollars) of k tickets that sold for $18 per ticket and n tickets that sold for $30 per ticket.
A. T = 18k - 30n B. T = 30k + 18n C. T = 48kn D. T = 18k + 30n
Multiply or divide as indicated.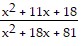 ?
? 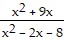
A. 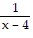
B. 
C. 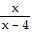
D.