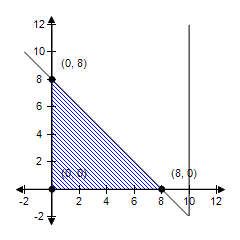
The linear programming problem has an unusual characteristic. Select a graph of the solution region for the problem and describe the unusual characteristic. Find the minimum value of the objective function (if possible) and where it occurs.
?
Objective function:
?
z = -x + 2y
?
Constraints:
?
x ? 0
y ? 0
x ? 10
x + y ? 8
?
A. ?
The constraint x ? 10 is extraneous. Minimum at (0, 8): 16
B.
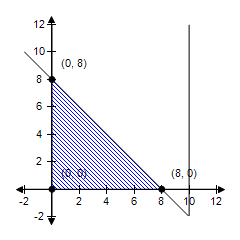
The constraint x ? 10 is extraneous. Minimum at (8, 0): -8
C.
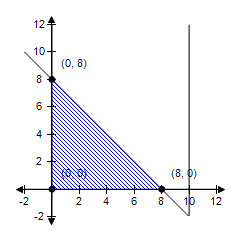
The constraint x ? 10 is extraneous. No minimum.
D.
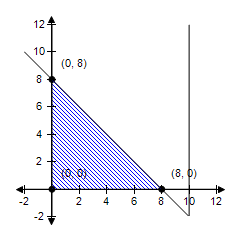
The constraint x ? 10 is extraneous. Minimum at (8, 8): 8
E.
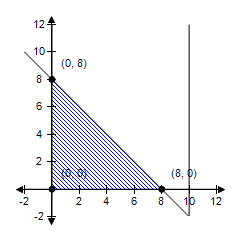
The constraint x ? 10 is extraneous. Minimum at (0, 0): 0
Answer: B
You might also like to view...
Determine if the given function y = f(x) is a solution of the accompanying differential equation.Differential equation: 2xy' + 2y = cos xInitial condition: y(?) = 0Solution candidate: y = 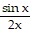
A. Yes B. No
Write in radical form. Assume all variables represent positive real numbers.5k-4/3
A. 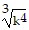
B. 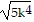
C. 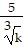
D. 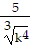
Write the word phrase as an algebraic expression. Use x to represent the unknown number.The product of 4 and a number
A. 4 + x
B. 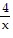
C. 4 - x
D. 4x
Determine the coordinates of the indicated point on the graph. 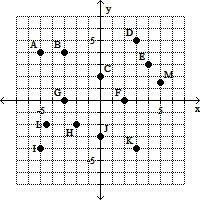 B
B
A. (4, 3) B. (-3, 4) C. (3, 4) D. (4, -3)