Find a particular solution of the differential equation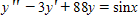 
.
?
A.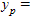 
?
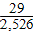
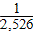
sinx + 
cosx
B. ??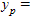
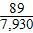
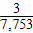
sinx + 
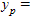
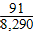
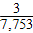
cosx
C. ??
sinx + 
cosx
D. ??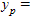
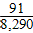
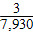
sinx + 
cosx
E. ??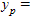
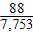
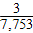
sinx + 
cosx
Answer: A
You might also like to view...
Solve the problem.According to a country's census, the population (to the nearest million) was 264 in Year 0 and 288 in Year 10. The projected population for Year 50 is 434. To construct a logistic model, both the growth and carrying capacity must be estimated. (a) Estimate r by assuming that t = 0 corresponds to Year 0 and that the population between Year 0 and Year 10 is exponential; that is, the population is given by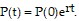 
Round the value of r to four decimal places, if necessary.(b) Write the solution to the logistic equation using the estimated value of r and use the projected value P(50) = 434 million to find an estimation for the value of the carrying capacity K. Round to
the nearest million. A. (a) r = -1.0087 (b) K = 254 million B. (a) r = 0.0087 (b) K = -2390 million C. (a) r = 1.0087 (b) K = -2290 million D. (a) r = -0.0087 (b) K = 154 million
Graph the equation.y = -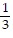 
x + 4
A.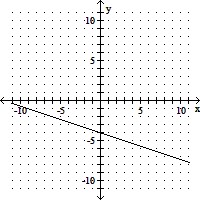 
B.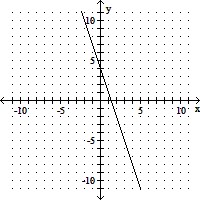 
C.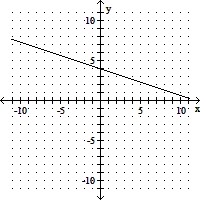 
D.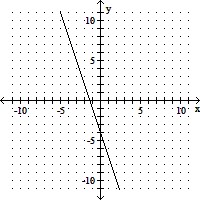 
Solve the absolute value equation.|x| = 3
A. {3, -3} B. {9} C. {3} D. {-3}
Simplify the factorial expression.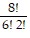
A. 8 B. 0! C. 28 D. 1