Answer the question.The graph below shows the level curves of a differentiable function f(x, y) (thin curves) as well as the constraint g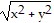(x, y) = 
- 
= 0 (thick circle). Using the concepts of the orthogonal gradient theorem and the method of Lagrange multipliers, estimate the coordinates corresponding to the constrained extrema of f(x,y).
A. (1.3, 0.7), (-1.3, 0.7), (-1.3,-0.7), (1.3,-0.7)
B. (1.5, 0.2), (0.7, 1.3), (-1.5, 0.2), (-0.7, 1.3), (-1.5, -0.2), (-0.7, -1.3), (1.5, -0.2), (0.7, -1.3)
C. (1.1, 1.1), (-1.1, 1.1), (-1.1,-1.1), (1.1,-1.1)
D. (1.5, 0), (0, 1.5), (-1.5, 0), (0, -1.5)
Answer: A
You might also like to view...
Solve the problem.Find a formula for the distance from the point P(x, y, z) to the yz plane.
A. 
B. y
C. x
D. z
______ is the process of evaluating a firm's credit policy to determine whether a shift in its customers' payment patterns has occurred.
A. Receivables monitoring B. Accounts payables monitoring C. Concentration banking D. Customer maintenance E. Purchasing subsidization
Graph the circle.x2 + (y - 6)2 = 9
A.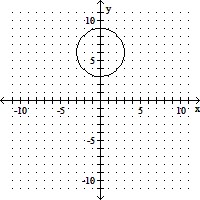 
B. 
C.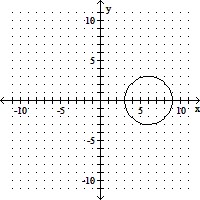 
D.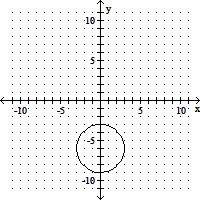 
Provide an appropriate response.Rounding can be used to approximate an answer.
A. True B. False