Solve the following quadratic application using the quadratic formula.The diagonal of a painting measures 11 feet. If the width of the painting is 3 feet more than the height, find the dimensions of the painting. (Use the Pythagorean Theorem.) Round to the nearest tenth.
A. The height of the painting is 6.1 feet, and the width of the painting is 26.3 feet.
B. The height of the painting is 6.1 feet, and the width of the painting is 9.1 feet.
C. The height of the painting is 4.3 feet, and the width of the painting is 9.1 feet.
D. The height of the painting is 9.1 feet, and the width of the painting is 6.1 feet.
Answer: B
You might also like to view...
Write the polynomial in standard form and identify the degree and leading coefficient of the polynomial. ? 6 ?
A. 6-xDegree: 0 ; Leading coefficient: 6 B. ?6?Degree: 0 ; Leading coefficient: 6 C. ?6?Degree: 6; Leading coefficient: 6 D. ?6x?Degree: 1; Leading coefficient: 6 E. ?6+x?Degree: 0 ; Leading coefficient: 6
Round the money amount to the specified place.$31.59 to the nearest dollar.
A. $31.6 B. $40 C. $32 D. $31
For the polynomial function find the following: (i) Degree of the polynomial; (ii) All x intercepts; (iii) The y intercept.y = 4x + 1
A. (i) 1
(ii) 1
(iii)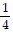 
B. (i) 1
(ii)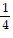 
(iii) 1
C. (i) 1
(ii) -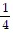 
(iii) 1
D. (i) 1
(ii) - 4
(iii) 4
Solve the problem.The number of centimeters, d, that a spring is compressed from its natural, uncompressed position is given by the formula d =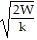 
, where W is the number of joules of work done to move the spring and k is the spring constant. Solve this equation for W. Use the result to determine the work needed to move a spring 8 centimeters if it has a spring constant of 0.6.
A. W =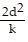 
; 213.3 joules
B. W = 
; 19.2 joules
C. W = 
; 5.8 joules
D. W = 2d2k; 76.8 joules