Solve the problem.Consider the pair of differential equations that model a predator-prey system with populations x and y. x'(t) = -5x + xy y'(t) = 2y - xy(a) Find the lines along which x'(t) = 0,(b) find the lines along which y'(t) = 0,(c) find the equilibrium points for the system.
A. (a) x' = 0 along the lines x =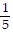 
and y = 0
(b) y' = 0 along the lines y =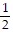 
and x = 0
(c) (0, 0) and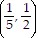 
B. (a) x' = 0 along the lines x = 0 and y = 5
(b) y' = 0 along the lines y = 0 and x = 2
(c) (0, 0) and (2, 5)
C. (a) x' = 0 along the lines x = 5 and y = 0
(b) y' = 0 along the lines y = 2 and x = 0
(c) (0, 0) and (5, 2)
D. (a) x' = 0 along the lines x = 0 and y =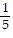 
(b) y' = 0 along the lines y = 0 and x = 
(c) (0, 0) and 
Answer: B
You might also like to view...
Provide an appropriate response.If A is a 6 × 7 matrix and A+ K = A, what can you say about K?
A. K is a 6 × 7 matrix and all entries of K are equal to 0. B. K is a 6 × 7 matrix and each of its entries is the negative of the corresponding entry of A. C. K is a 7 × 6 matrix and each of its entries is the negative of the corresponding entry of A. D. K is a 7 × 6 matrix and all entries of K are equal to 0.
Solve the equation.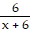
= 
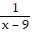
A. 3
B. -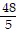 
C.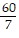 
D. 12
Determine whether the given ordered pair is a solution of the system.(-3, 3)4x - y = -92x + 4y = 6
A. not a solution B. solution
Determine whether the equation is a proportion.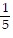
= 
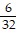
A. It is a proportion. B. It is not a proportion.