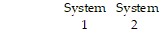Solve the linear programming problem.The Acme Class Ring Company designs and sells two types of rings: the VIP and the SST. They can produce up to 24 rings each day using up to 60 total man-hours of labor. It takes 3 man-hours to make one VIP ring and 2 man-hours to make one SST ring. How many of each type of ring should be made daily to maximize the company's profit, if the profit on a VIP ring is $40 and on an SST ring is $35?
A. 16 VIP and 8 SST
B. 14 VIP and 10 SST
C. 18 VIP and 6 SST
D. 12 VIP and 12 SST
Answer: D
You might also like to view...
Divide.-500 ÷ (-8)
A. -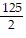 
B.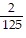 
C.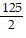 
D. 625
Solve the problem.The rate at which an assembly line worker's efficiency E (expressed as a percent) changes with respect to time t is given by 
where t is the number of hours since the worker's shift began. Assuming that 
when t = 1, find and expression for E.
A. E = 65t - 4t2 + 25 B. E = 65t - 2t2 + 151 C. E = 65t - 2t2 + 88 D. E = 65t - 2t2 + 25
Use a graphing utility to graph the function over the indicated interval and approximate any local maxima and local minima. Determine where the function is increasing and where it is decreasing. If necessary, round answers to two decimal places.f(x) = x5 - x2; (-2, 2)
What will be an ideal response?
Solve the problem.The final grade for an algebra course is determined by grades on the midterm and final exam. The grades for four students and two possible grading systems are modeled by the following matrices. src="https://sciemce.com/media/4/ppg__10625191827__f1q45g6.jpg" style="vertical-align: -15.0px;" />Find the final course score for Student 3 for both grading System 1 and System 2.
A. System 1: 65.8; System 2: 98.2
B. System 1: 82.4; System 2: 82
C. System 1: 77.2; System 2: 76
D. System 1: 44.2; System 2: 53
