Write the system of inequalities that describes the possible solutions to the problem.The Pen-Ink Company manufactures two ballpoint pens: silver and gold. The silver requires 9 minutes in a grinder and 8 minutes in a bonder. The gold requires 11 minutes in a grinder and 8 minutes in a bonder. The grinder can be run no more than 390 minutes per day and the bonder no more than 180 minutes per day. Let x represent the number of silver pens, and let y represent the number of gold pens. Including the system inequalities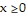 
and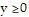 
, find the remaining
inequalities that best represent this company's daily production of silver and gold pens.
A. 0 ? 17x + 19y ? 570
B. 9x + 8y ? 390, 11x + 8y ? 180
C. x + y ? 390, x + y ? 180, x + y ? 570
D. 9x + 11y ? 390, 8x + 8y ? 180
Answer: D
You might also like to view...
Solve.How many different 4-letter radio-station call letters can be made if the first letter must be K or W, letters may be repeated, and the call letters cannot end in an O?
A. 35,152 B. 456,976 C. 33,800 D. 16,900
Use the graph to find the horizontal asymptote, if any, of the function.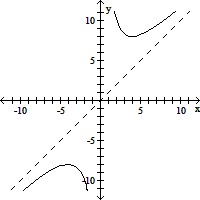
A. y = -8 B. y = 8 C. y = 0 D. none
Determine whether the given ordered pair satisfies the inequality.y ? -x: (-25, 25)
A. Yes B. No
Find two sets of parametric equations for the given rectangular equation.y = 8 - (x - 7)3
What will be an ideal response?