Solve the problem.The delivery of a drug (such as an antibiotic) through an intravenous line may be modeled by the differential equation  where m(t) is the mass of the drug in the blood at time
where m(t) is the mass of the drug in the blood at time  k is a constant that describes the rate at which the drug is absorbed, and I is the infusion rate. Let
k is a constant that describes the rate at which the drug is absorbed, and I is the infusion rate. Let  and
and  For what initial values
For what initial values
src="https://sciemce.com/media/4/ppg__wesa0610191635__f1q75g5.jpg" alt="" style="vertical-align: -4.0px;" /> are solutions increasing? decreasing? What is the equilibrium solution?
A. increasing for A > 125 and decreasing for A < 125; m(t) = 125
B. increasing for A < 125 and decreasing for A > 125; m(t) = 125
C. increasing for A < 125 and decreasing for A > 125; m(t) = 0
D. increasing for A > 125 and decreasing for A < 125; m(t) = 0
Answer: B
Mathematics
src="https://sciemce.com/media/4/ppg__wesa0610191635__f1q75g5.jpg" alt="" style="vertical-align: -4.0px;" /> are solutions increasing? decreasing? What is the equilibrium solution?
A. increasing for A > 125 and decreasing for A < 125; m(t) = 125
B. increasing for A < 125 and decreasing for A > 125; m(t) = 125
C. increasing for A < 125 and decreasing for A > 125; m(t) = 0
D. increasing for A > 125 and decreasing for A < 125; m(t) = 0
Answer: B
You might also like to view...
Express the vector as a product of its length and direction. - i -
i - 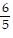 j +
j +  k
k
A. 

B. 
C. 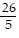 (-i - j + k)
(-i - j + k)
D. 
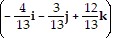
Evaluate the combination.
A. 36 B. 9 C. 1 D. 0
Divide using synthetic division.
A. m2 + 5m + 6 B. 7m2 + 4m + 4 C. m2 + 4m + 7 D. 7m2 - 4m + 4
Find the largest open interval where the function is changing as requested.Decreasing y = 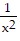 + 7
+ 7
A. (-7, 0) B. (7, ?) C. (0, ?) D. (-7, 7)