For each of (a)–(c) below, either draw a graph with the specified properties or else explain why no such graph exists.
(a) Graph with six vertices of degrees 1, 1, 2, 2, 2, and 3.
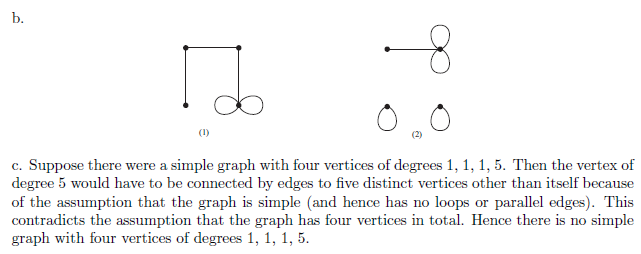
(b) Graph with four vertices of degrees 1, 2, 2, and 5.
(c) Simple graph with four vertices of degrees 1, 1, 1, and 5.
a. Given any graph, the total degree of the graph (being twice the number of edges) is an even
number. Thus there is no graph with six vertices of degrees 1, 1, 2, 2, 2, and 3 because its
total degree would be 1 + 1 + 2 + 2 + 2 + 3 = 11, an odd number.
You might also like to view...
Provide an appropriate response.Fred and Sue want to fence in a rectangular area in their yard for a vegetable garden. Suppose that they have 30 feet of fencing. Sue tells Fred that she wants to put up the fence in such a way as to obtain a rectangular garden with the largest possible perimeter. Fred replies that the perimeter will be the same for any rectangular garden that they construct as long as they use all 
of the fencing. Is Fred correct? Explain.
What will be an ideal response?
Determine the average rate of change for the function.F(x) = -7
A. 7
B. 0
C. -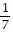 
D. -7
Convert the angle to decimal degrees and round to the nearest hundredth of a degree.43°38'
A. 43.63° B. 43.76° C. 43.38° D. 44.63°
Find the component form of the indicated vector.Let u =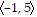 
, v =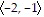 
. Find -u - v.
A. 
B.
 |
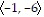C.
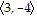
D.
 |
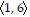