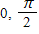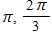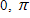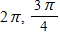Find a function P(x) defined by a polynomial of degree 3 with real coefficients that satisfies the given conditions.Zeros of -3, 2, 4 and P(1) = 12
A. P(x) = x3 + 3x2 - 9x + 20
B. P(x) = x3 - 3x2 - 10x + 24
C. P(x) = x3 - 3x2 - 9x + 20
D. P(x) = x3 - 3x2 - 10x - 24
Answer: B
Mathematics
You might also like to view...
Solve the problem.The amount of particulate matter left in solution during a filtering process decreases by the equation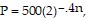 
where n is the number of filtering steps. Find the amounts left for n = 0 and n = 5. (Round to the nearest whole number.)
A. 500, 125 B. 500, 2000 C. 1000, 125 D. 500, 16
Mathematics
Perform the indicated operation.(x + 6)(x3 + 7x - 2)
A. x4 + 6x3 + 7x2 + 44x + 12 B. x4 + 6x3 + 7x2 + 40x - 12 C. x4 + 7x2 - 2x + 6 D. x3 + 13x2 + 40x - 12
Mathematics
Find the LCM of the set of numbers.12, 30
A. 60 B. 42 C. 30 D. 360
Mathematics
Find all solutions of the following equation in the interval [0, 2?).
?
?
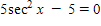
A. 
B. ?
C. ?
D. ?
E. ?
Mathematics