(a) find the equilibrium value(s) of the differential equation;
(b) access the stability of each equilibrium value;
(c) determine the point(s) of inflection;
(d) sketch sample solutions of the differential equation.
(a) y = ?4, 5
(b) Asymptotically stable, unstable
(c) y = 1/2
(d) 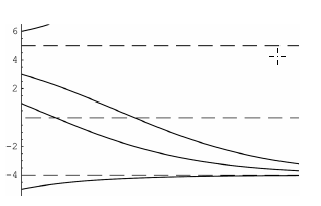
You might also like to view...
Provide an appropriate response.The region shown here is to be revolved about the x-axis to generate a solid. Which of the methods (disk, washer, shell) could you use to find the volume of the solid? How many integrals would be required in each case?

What will be an ideal response?
The given graph represents a translation of the graph of y = x2. Write the equation of the graph. 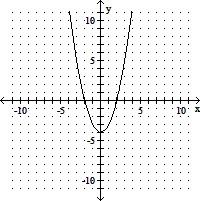
A. y = (x - 4)2 + 3 B. y = (x - 4)2 C. y = x2 - 4 D. y = (x + 4)2
Decide whether the equation is or is not an identity.sin (? + 2?) = sin ?
A. Identity B. Not an identity
Solve.Find 8 subtracted from 85.
A. 78 B. 87 C. 77 D. 76
