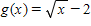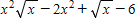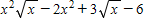Suppose a study reports that the average price for a gallon of self-serve regular unleaded gasoline is $3.16. You believe that the figure is higher in your area of the country. You decide to test this claim for your part of the United States by randomly calling gasoline stations. Your random survey of 25 stations produces the following prices (all in dollars). Assume gasoline prices for a region are normally distributed. Did the data you obtained provide enough evidence to reject the claim?
Use a 1% level of significance.
Make sure you clearly state both the null and the alternative hypotheses in full sentences. Following your calculations, clearly state the conclusion in the same manner (do not simply say “accept/reject null”) and explain how you arrived at this conclusion (based on which metrics).
3.27
3.3
3.16
3.15
3.11
3.05
3.54
3.25
3.05
3.11
3.13
3.15
3.27
3.14
3.14
3.2
3.3
3.09
3.05
3.07
3.37
3.34
3.35
3.35
3.1
Ans: H0: Mean cost of a gallon of self-serve regular unleaded gasoline = $3.16. Ha: Mean cost of a gallon of self-serve regular unleaded gasoline ? $3.16. Sample mean of data = 3.1852 Sample standard deviation = 0.10251504 t = sample mean - average expected / s / SQRT(sample size) = 3.1852 - 3.16 / (0.10251504/ sqrt (25)) = 1.2291 p-value = (24 degrees of freedom, two tailed test, 0.01 level of confidence) = .8845 p-value is not < than .01, do not reject the null hypothesis => This data does not show that the average of a gallon of self-serve regular unleaded gasoline is statistically different than $3.16.
You might also like to view...
Solve for the missing numbers. Markup is based on selling price. Round dollar amounts to the nearest cent.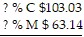
100% S $ ?
A. 
100% S $ 39.89
B.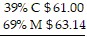 
100% S $166.17
C. 
100% S $166.17
D.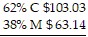 
100% S $166.17
Find 
of the functions.
?
, 
?
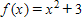
A. 
B. 
C. 
D. 
E. 
Solve the problem.Since 2011, compact SUV sales have been on the rise, while sedan sales have decreased. Let V(t) represent the number (in millions) of SUVs sold during the year that is t years since 2007. Let S(t) represent the number (in millions) of sedans sold during the year that is t years since 2007. The equations for V and S are given below.V(t) = 0.12t - 0.22 SUVs S(t) = -0.10t + 1.43 Sedans i) What are the slopes of V and S? What do they mean in terms of car sales?ii) Estimate in which year the same number of SUVs were sold as sedans. How many were sold of each?
What will be an ideal response?
Find the midpoint of the line segment with the given end points.(3, -5) and (5, -7)
A. 
B. (-2, 2)
C.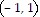 
D. (8, -12)