Use the Principle of Mathematical Induction to show that the statement is true for all natural numbers n.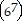 n = 67n
n = 67n
What will be an ideal response?
First we show that the statement is true when n = 1.
For n = 1, we get 67 = 6(7?1) = 67
This is a true statement and Condition I is satisfied.
Next, we assume the statement holds for some k. That is,
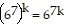 is true for some positive integer k.
is true for some positive integer k.
We need to show that the statement holds for k + 1. That is, we need to show that
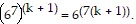
So we assume that 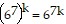 is true and multiply the next term,
is true and multiply the next term, 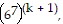 to both sides of the equation.
to both sides of the equation.
 k
k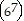 (k + 1) = 67k
(k + 1) = 67k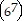 (k + 1)
(k + 1)
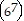 (k + (k + 1)) = 67k
(k + (k + 1)) = 67k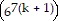
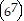 (2k + 1) = 6(7k + 7k + 7))
(2k + 1) = 6(7k + 7k + 7))
6(7(2k + 1)) = 6(7(2k + 1))
Condition II is satisfied. As a result, the statement is true for all natural numbers n.
You might also like to view...
Find the product or quotient, using trigonometric form. Write the answer in the form a + bi.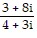
A. 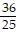 +
+ 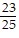 i
i
B. 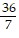 -
-  i
i
C. - 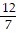 -
- 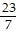 i
i
D. - 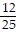 -
-  i
i
Solve the problem.Assume it costs 30 cents to mail a letter weighing one ounce or less, and then 28 cents for each additional ounce or fraction of an ounce. Write a piecewise-defined function P(x) that represents the cost, in cents, of mailing a letter weighing between 0 and 3 ounces.
A. P(x) = {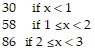
B. P(x) = {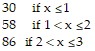
C. P(x) = {
D. P(x) = {
Provide an appropriate response.(x + 1)(x2 + 3x - 5) - 3x2 =
A. -2x3 + 4x2 - 2x - 5 B. -3x5 - 12x4 + 6x3 + 15x2 C. -2x2 + 4x - 4 D. x3 + x2 - 2x - 5 E. x3 + 4x2 - 2x - 5
Solve.Frank can type a report in 3 hours and James takes 4 hours. How long will it take the two of them typing together?
A. 4 hr
B. 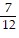 hr
hr
C. 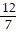 hr
hr
D. 12 hr