Use mathematical induction to prove the following.12 + 42 + 72 + . . . + (3n - 2)2 = 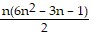
What will be an ideal response?
Answers may vary. One possibility:
Sn: 12 + 42 + 72 + . . . + (3n - 2)2 = 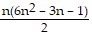
S1: 12 = 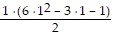
Sk: 12 + 42 + 72 + . . . + (3k - 2)2 = 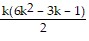
Sk+1: 12 + 42 + 72 + . . . + (3k - 2)2 + [3(k + 1) - 2]2 = 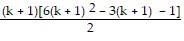
1. Basis step: Since 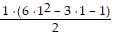 =
= 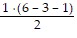 =
= 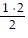 = 1 = 12, S1 is true.
= 1 = 12, S1 is true.
2. Induction step: Let k be any natural number. Assume Sk. Deduce Sk+1.
12 + 42 + 72 + . . . + (3k - 2)2 = 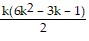
12 + 42 + 72 + . . . + (3k - 2)2 + [3(k + 1) - 2]2 =  + [3(k + 1) - 2]2
+ [3(k + 1) - 2]2
= 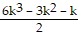 + (3k + 1)2
+ (3k + 1)2
= 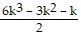 + (9k2 + 6k + 1)
+ (9k2 + 6k + 1)
= 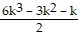 +
+ 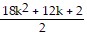
= 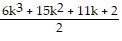
= 
= 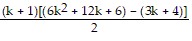
= 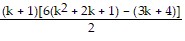
= 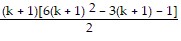 .
.
You might also like to view...
Factor completely. If the polynomial cannot be factored, write "prime."x2 + 8x - 20
A. (x - 10)(x + 2) B. (x + 10)(x - 2) C. (x - 10)(x + 1) D. Prime
Solve. The FDA approves a new drug and has confirmed by independent research that the strength of the reaction to the drug is given by the expression 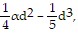 where d is the dosage of the drug and ? is a constant. Factor this expression.
where d is the dosage of the drug and ? is a constant. Factor this expression.
A. d2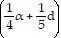
B.  (? - d)
(? - d)
C. d2
D. 

Find the exact value of the expression without using a calculator or table.arcsec ( )
)
A. 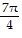
B.  ± 2?n,
± 2?n,  ± 2?n
± 2?n
C. 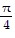
D. 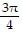
Arrange in order from smallest to largest.0.09, 0.04, 0.049, 0.094
A. 0.04, 0.09, 0.049, 0.094 B. 0.094, 0.049, 0.09, 0.04 C. 0.049, 0.094, 0.04, 0.09 D. 0.04, 0.049, 0.09, 0.094