Solve the problem.Suppose that an insect population density, in thousands, during year n can be modeled by the recursively defined sequence: 
.Use technology to graph the sequence for n = 1 , 2 , 3 , ........., 20 . Describe what happens to the population density function.
A. The insect population increases every year.
B. The insect population stabilizes near 14.36 thousand.
C. The insect population stabilizes near 11.16 thousand.
D. The insect population stabilizes near 13.35 thousand.
Answer: B
You might also like to view...
Using Green's Theorem, find the outward flux of F across the closed curve C.F = ln (x2 + y2) i + tan-1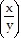 
j; C is the region defined by the polar coordinate inequalities 
and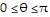 
A. 63 B. 65 C. 0 D. 126
The figure shows the velocity v or position s of a body moving along a coordinate line as a function of time t . Use the figure to answer the question. s (m)
When is the body moving forward?
A. 0 < t < 1, 3 < t < 4, 5 < t < 7 B. 0 < t < 3, 3 < t < 5, 5 < t < 8 C. 0 < t < 8 D. 0 < t < 1, 3 < t < 4, 5 < t < 7, 9 < t < 10
Find the polynomial of lowest degree that will approximate F(x) throughout the given interval with an error of magnitude less than than 10-3.F(x) =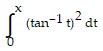 
, [0, 0.5]
A.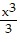 
- 
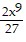
B.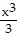 
- 
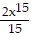
C.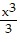 
- 
D.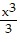 
- 
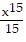
Find the focus and directrix of the parabola.-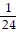 
x2 = y
A. (0, -6); y = 6 B. (-12, 0); x = 6 C. (0, 6); y = -6 D. (0, -6); y = -6