Use the Principle of Mathematical Induction to show that the statement is true for all natural numbers n.1 ? 2 + 2 ? 3 + 3 ? 4 + . . . + n(n + 1) =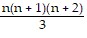 
What will be an ideal response?
First we show that the statement is true when n = 1.
For n = 1, we get 2 = 
= 2.
This is a true statement and Condition I is satisfied.
Next, we assume the statement holds for some k. That is,
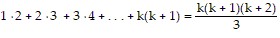is true for some positive integer k.
We need to show that the statement holds for k + 1. That is, we need to show that
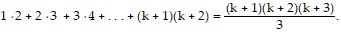
So we assume that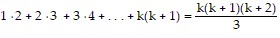 
is true and add the next term, 
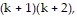to both sides of the equation.
1 ? 2 + 2 ? 3 + 3 ? 4 + . . . + k(k + 1) + (k + 1)(k + 2) =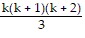 
+ (k + 1)(k + 2)
= 
+ 
= 
= 
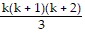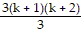
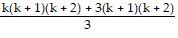
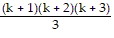
Condition II is satisfied. As a result, the statement is true for all natural numbers n.
You might also like to view...
Solve the problem that involves probabilities with dependent events. Elise has put 5 cans (all of the same size) on her kitchen counter; 2 cans of vegetables, 2 cans of soup , and 1 can of peaches. Her son, Ryan, takes the labels off the cans and throws them away. Elise then chooses 2 cans (without replacement) at random to open. Find the probability that she will open at least 1 can of vegetables.
A. 
B.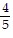 
C.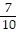 
D.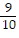 
Find the requested value.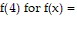
{6x + 6 if x ? 04 - 3x if 0 < x < 3x if x ? 3
A. 4 B. -8 C. 3 D. 30
Convert the temperature algebraically. Round the answer to one decimal place.110°C to Fahrenheit
A. 230°F B. 79.4°F C. 43.8°F D. 166°F
Graph the linear function.g(x) =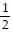 
x - 6
A.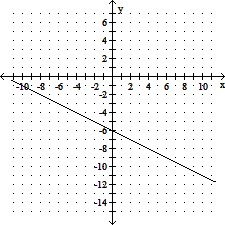 
B. 
C.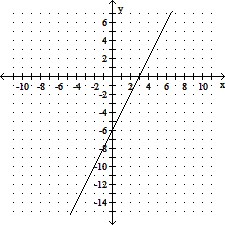 
D. 