Use mathematical induction to prove that the statement is true for every positive integer n.2 ? 4 + 3 ? 5 + 4 ? 6 + ... + (n + 1)(n + 3) = 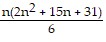
What will be an ideal response?
Answers will vary. One possible proof follows.
a). Let n = 1. Then, 2 ? 4 = 8 = 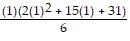 =
= 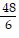 = 8. Thus, the statement is true for n = 1.
= 8. Thus, the statement is true for n = 1.
b). Assume that the statement is true for n = k:
Sk = 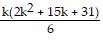
Also, if the statement is true for n = k + 1, then
Sk+1 = Sk + ((k + 1) + 1)((k + 1) + 3) = 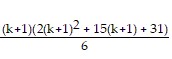
Substitute the expression for Sk into the one for Sk+1:
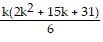 + ((k + 1) + 1)((k + 1) + 3) =
+ ((k + 1) + 1)((k + 1) + 3) = 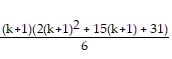
By collecting all terms on the left-hand side over a common denominator and then expanding numerators on both sides, one can show that the equality holds.
Since the equality holds, the statement is true for n = k + 1 as long as it is true for n = k. Furthermore, the statement is true for n = 1. Thus, it is true for all natural numbers n.
You might also like to view...
Perform the operation.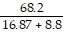
A. 0.45939538 B. 2.65679782 C. 130.7425 D. 11.7926793
Find the requested characteristic.Find the period for the graph of f(t) = - tan  .
.
A. 
B. 
C. 7?
D. 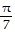
Solve the equation by completing the square.2x2 + 12x = - 7
A. 
B. 
C. 
D. 
Decide whether the limit exists. If it exists, find its value.lim f(x)x?0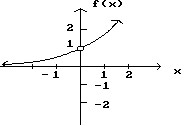
A. -1 B. Does not exist C. 1 D. 0