Use the Principle of Mathematical Induction to show that the statement is true for all natural numbers n.1 ? 1 + 2 ? 1 + 3 ? 1 + . . . + n = 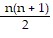
What will be an ideal response?
First we show that the statement is true when n = 1.
For n = 1, we get 1 = 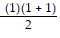 = 1.
= 1.
This is a true statement and Condition I is satisfied.
Next, we assume the statement holds for some k. That is,
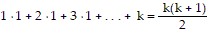 is true for some positive integer k.
is true for some positive integer k.
We need to show that the statement holds for k + 1. That is, we need to show that
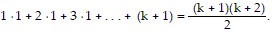
So we assume that 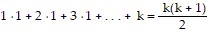 is true and add the next term,
is true and add the next term, 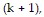 to both sides of the equation.
to both sides of the equation.
1 ? 1 + 2 ? 1 + 3 ? 1 + . . . + k + (k + 1) = 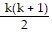 + (k + 1)
+ (k + 1)
= 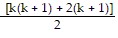
= 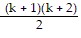
Condition II is satisfied. As a result, the statement is true for all natural numbers n.
You might also like to view...
Solve the problem.At time t ? 0, the velocity of a body moving along the s-axis is  When is the body's velocity increasing?
When is the body's velocity increasing?
A. t > 4.5 B. t < 8 C. t < 4.5 D. t > 8
Provide an appropriate response.Determine the volume of the given figure
A. 224 in3 B. 448 in3 C. 12,544 in3 D. 896 in3
Graph the exponential function.f(x) = 5x + 1 
A. 
B. 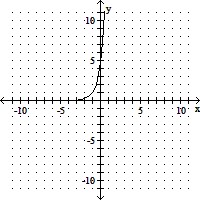
C. 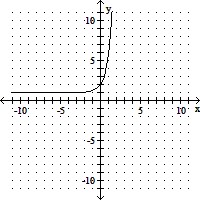
D. 
Solve the problem.In Country X, the average hourly wage in dollars from 1960 to 2010 can be modeled by f(x) = 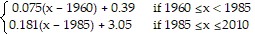 Use f to estimate the average hourly wages in 1965, 1985, and 2005.
Use f to estimate the average hourly wages in 1965, 1985, and 2005.
A. $0.77, $2.27, $6.67 B. $0.77, $3.05, $6.67 C. $3.43, $0.39, $6.67