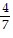Use mathematical induction to prove that the statement is true for every positive integer n.6 + 2 ? 6 + 3 ? 6 + . . . + 6n = 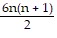
What will be an ideal response?
Answers will vary. One possible proof follows.
a). Let n = 1. Then, 8 = 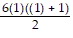 =
= 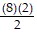 = 8. Thus, the statement is true for n = 1.
= 8. Thus, the statement is true for n = 1.
b). Assume the statement is true for n = k:
Sk = 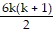
Also, if the statement is true for n = k + 1, then
Sk+1 = Sk + 8(k + 1) = 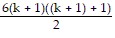
Subtract to obtain:
Sk+1 - Sk = 8(k + 1) = 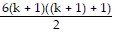 -
- 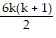
Expand both sides and collect like terms:
8k + 8 = 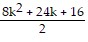 -
-  =
= 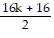 = 8k + 8
= 8k + 8
Since the equality holds, then the statement is true for n = k + 1 as long as it is true for n = k. Furthermore, the statement is true for n = 1. Therefore, the statement is true for all natural numbers n.
You might also like to view...
Solve the problem.Find the number of years for $14,100 to grow to $16,600 at 3% compounded semiannually. Round to the nearest tenth of a year.
A. 5.5 yr B. 5.4 yr C. 4.6 yr D. 6.6 yr
If an argument reads p ? q q ? p, then we can conclude p _______________ q .
Fill in the blank(s) with the appropriate word(s).
Solve the system of equations by Gauss-Jordan elimination.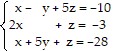
A. {(-3, 0, -5)} B. {(-3, -5, 0)} C. {(0, -5, -3)} D. ?
Find the probability.One digit from the number 5,282,772 is written on each of seven cards. What is the probability of drawing a card that shows 5, 2, or 8?
A. 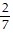
B. 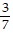
C. 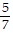
D.