Use Gauss-Jordan elimination to solve the linear system and determine whether the system has a unique solution, no solution, or infinitely many solutions. If the system has infinitely many solutions, describe the solution as an ordered triple involving variable z.4x - y + 3z=12x + 4y + 6z=-325x + 3y + 9z=20
A. (8, -7, -2)
B. (2, -7, -1)
C. no solution
D. (-8, -7, 9)
Answer: C
Mathematics
You might also like to view...
Solve for the indicated variable.F =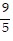 
C + 32 for C
A. C =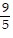 
(F - 32)
B. C = 
C. C = 
D. C =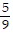 
(F - 32)
Mathematics
Factor completely. If unfactorable, indicate that the polynomial is prime.49 - w2
A. (7 - w)2 B. prime C. (7 + w)2 D. (7 - w)(7 + w)
Mathematics
Change the logarithmic expression to an equivalent expression involving an exponent.ln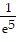 
= -5
A.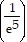 
e = -5
B. e-5 =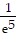 
C.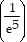 
-5 = e
D. -5e =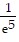 
Mathematics
Determine the values of the parameter s for which the system has a unique solution, and describe the solution.5sx1 + 9x2 = -35x1 + sx2 = 4
A. s ? 3; x1 =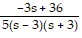 
and x2 =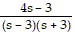 
B. s ? ± 3; x1 =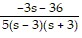 
and x2 =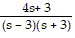 
C. s ? ± 9; x1 = -3s - 36 and x2 = 4s + 3
D. s ? ± 5; x1 =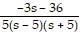 
and x2 =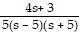 
Mathematics