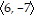Solve the problem.A small frictionless cart, attached to the wall by a spring, is pulled 10 cm back from its rest position and released at time t = 0 to roll back and forth for 4 sec. Its position at time t is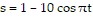 
. What is the cart's maximum speed? When is the cart moving that fast? What is the magnitude of of the acceleration then?
A. ? ? 3.14 cm/sec; t = 0.5 sec, 1.5 sec, 2.5 sec, 3.5 sec; acceleration is 0 cm/sec2
B. 10? ? 31.42 cm/sec; t = 0 sec, 1 sec, 2 sec, 3 sec; acceleration is 0 cm/sec2
C. 10? ? 31.42 cm/sec; t = 0.5 sec, 2.5 sec; acceleration is 1 cm/sec2
D. 10? ? 31.42 cm/sec; t = 0.5 sec, 1.5 sec, 2.5 sec, 3.5 sec; acceleration is 0 cm/sec2
Answer: D
You might also like to view...
Solve the problem.Find the equation of the plane perpendicular to the plane with equation x - 2y + 5z = 15 and the plane with equation3x + z = -7 and containing the point P = (-5, 0, -7).
A. x - 2y + 5z + 40 = 0 B. 3x + z + 22 = 0 C. -x + 7y + 3z - 16 = 0 D. -x + 7y + 3z + 16 = 0
Solve the equation.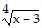
= 2
A. 625 B. 19 C. 11 D. 13
Make a line graph of the data.The following table shows the number of computer sales made at Computer Buy over five months. Use time on the horizontal scale for your line graph.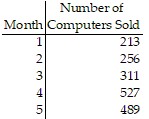
What will be an ideal response?
A vector v has initial point P and terminal point Q. Graph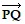 
and write 
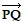as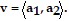 
P = (1, -2), Q = (7, -9)
A.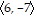 
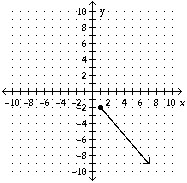
B. 
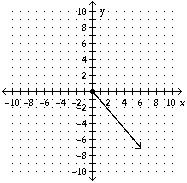
C.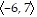 
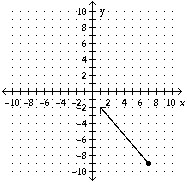
D. 
