Solve the problem using the quadratic formula.For a car traveling at x mph, stopping distance is estimated by the formula d(x) =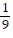 
x2 +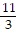 
x. Find a (maximum) safe speed for a stopping distance of 610 ft. Round your answer to the nearest mph.
A. 68 mph
B. 63 mph
C. 71 mph
D. 59 mph
Answer: D
You might also like to view...
Solve the problem. Write ratios in simplest form.The table below shows the amounts of pollutants (in parts per million) in a sample of rainwater. Find the ratio of pollutant A to pollutant B.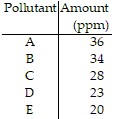 
A. 
B. 
C. 
D.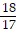 
Solve the problem.Let C = 900 + 40x be the cost to manufacture x items. Find the average cost per item to produce 30 items.
A. $1253 B. $70 C. $705 D. $698
Solve.In the United States, approximately 71 million of the 200 million cars and light trucks in service have driver-side air bags. In a parking lot containing 1000 cars and light trucks, how many would be expected to have driver-side air bags?
A. 305 cars and light trucks B. 405 cars and light trucks C. 355 cars and light trucks D. 455 cars and light trucks
?Use the position equation s = -16t2 + v0t + s0 to write a function that represents the situation and give the average velocity of the object from time t1 to time t2.An object is thrown upward from a height of 38 feet at a velocity of 84 feet per second. t1 = 1, t2 = 3
A. ?s= -16t2+ 38t + 84; avg. velocity = 79 ft/s B. ?s = -16t2+ 84t + 38; avg. velocity = 125 ft/s C. ?s = -16t2+ 38t + 84; avg. velocity = -26 ft/s D. ?s= -16t2+ 84t + 38; avg. velocity = 20 ft/s E. ?s= -16t2 + 84t + 38; avg. velocity = 40 ft/s