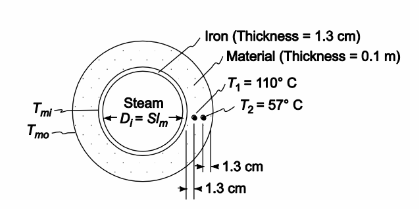
The thermal conductivity of a material can be determined in the following manner. Saturated steam 2.41 ? 105 N/m2 is condensed at the rate of 0.68 kg/h inside a hollow iron sphere that is 1.3 cm thick and has an internal diameter of 51 cm. The sphere is coated with the material whose thermal conductivity is to be evaluated. The thickness of the material to be tested is 10 cm and there are two thermocouples embedded in it, one 1.3 cm from the surface of the iron sphere and one 1.3 cm from the exterior surface of the system. If the inner thermocouple indicates a temperature of 110°C and the outer themocouple a temperature of 57°C, calculate (a) the thermal conductivity of the material surrounding the metal sphere, (b) the temperatures at the interior and exterior surfaces of the test
material, and (c) the overall heat transfer coefficient based on the interior surface of the iron sphere, assuming the thermal resistances at the surfaces, as well as the interface between the two spherical shells, are negligible.
GIVEN

FIND

ASSUMPTIONS
- Thermal resistance at the surface is negligible
- Thermal resistance at the interface is negligible
- The system has reached steady-state
- The thermal conductivities are constant
- One dimensional conduction radially
SKETCH
(a) The rate of heat transfer through the sphere must equal the energy released by the condensing steam:
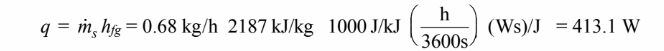
The thermal conductivity of the material can be calculated by examining the heat transfer between the thermocouple radii
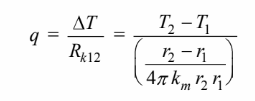
Solving for the thermal conductivity

(b) The temperature at the inside of the material can be calculated from the equation for conduction through the material from the inner radius, the radius of the inside thermocouple
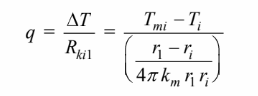
Solving for the temperature of the inside of the material

The temperature at the outside radius of the material can be calculated from the equation for conduction through the material from the radius of the outer thermocouple to the outer radius
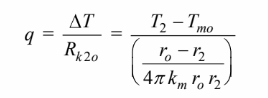
Solving for the temperature of the outer surface of the material

(c) The heat transfer through the sphere can be expressed as
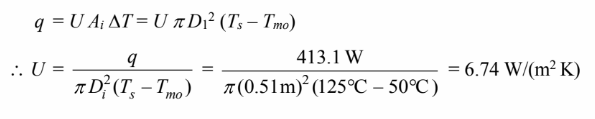
You might also like to view...
The molecules forming the DNA are shaped like a:
a. Coiled spiral c. Sphere b. Cube d. Long straight tube
Solve the system of equations by using the substitution method.2x + y = 123x + 2y = 16
Fill in the blank(s) with the appropriate word(s).
How is the fall zone for a forklift operation best defined?
a. A minimum of a 30-foot diameter circle around the forklift. b. Twice the length of the base of the forklift. c. Any area into which the lifted materials could potentially fall. d. Twice the width of the object being lifted.
Which international standards organization coordinates global communications networks and services and is actually a treaty organization?
A. IAB B. TIA C. ISO D. ITU