Use mathematical induction to prove that the statement is true for every positive integer n.9n > 9n - 1
What will be an ideal response?
Answers will vary. One possible proof follows.
a). Let n = 1. then, 91 = 9 > 91 - 1 = 90 = 1. So, the statement is true for n = 1.
b). Assume that the statement is true for n = k:
9k > 9k - 1
Multiply both sides by 9:
9 ? 9k = 9k + 1 > 9 ? 9k - 1 = 9k = 9(k + 1) - 1 or 9k + 1 > 9(k + 1) - 1
Since the statement is true for n = k + 1 as long as it is true for n = k, and since the statement is true for n = 1, then it is true for all natural numbers n.
You might also like to view...
Find all angles in [0°, 360°) that satisfy the equation.sec 4? = -2
A. 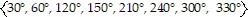
B. 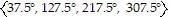
C. 
D. 
Use transformations of the graph of y = x4 or y = x5 to graph the function.f(x) =  x4
x4 
A. 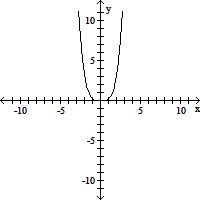
B. 
C. 
D. 
Graph the function.f(x) = -3 - ln x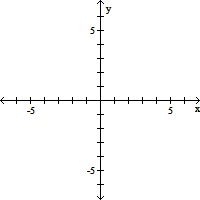
A. 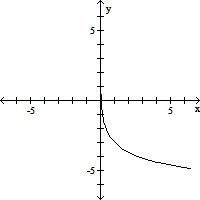
B. 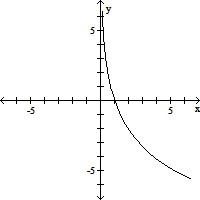
C. 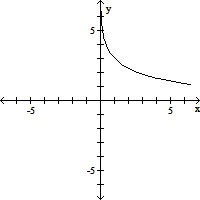
D. 
Match the correct graph to the given function.y = 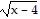
A. 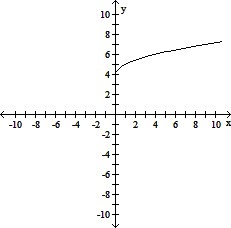
B. 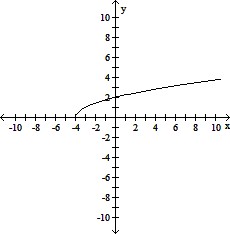
C. 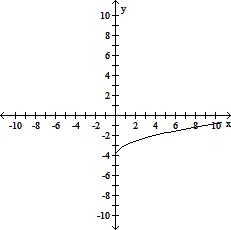
D.