For the polynomial, list each real zero and its multiplicity. Determine whether the graph crosses or touches the x-axis at each x -intercept.f(x) = 2(x - 6)(x - 2)3
A. -6, multiplicity 1, touches x-axis; -2, multiplicity 3
B. 6, multiplicity 1, touches x-axis; 2, multiplicity 3
C. 6, multiplicity 1, crosses x-axis; 2, multiplicity 3, crosses x-axis
D. -6, multiplicity 1, crosses x-axis; -2, multiplicity 3, crosses x-axis
Answer: C
You might also like to view...
Find the tangential and normal components of the acceleration.r(t) = (t - 7)i + (ln(sec t) - 8)j + 8k, -?/2 < t < ?/2
A. a = (cos t)T + (cos t)N B. a = (csc t)T + (sec t)N C. a = (sec2 t)T + (cos t)N D. a = (sec t tan t)T + (sec t)N
Solve. Express the result in scientific notation. Round to the nearest hundredth, if necessary.In one year, light travels 5.87 × 1012 miles. How far would light travel in 7 × 104 years?
A. 4.11 × 1016 miles B. 4.11 × 1017 miles C. 4.11 × 1049 miles D. 1.29 × 1016 miles
Find the center (h, k) and radius r of the circle. Graph the circle.2x2 + 2y2 - 8x + 16y + 22 = 0
A. (h, k) = (2, -4); r = 9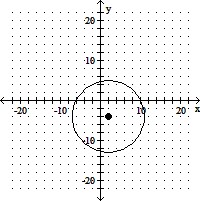
B. (h, k) = (-2, 4); r = 3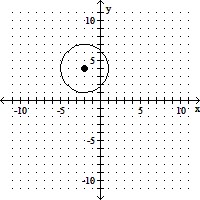
C. (h, k) = (2, -4); r = 3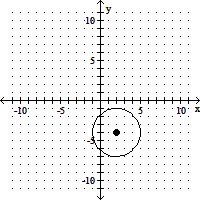
D. (h, k) = (-2, 4); r = 9
The equation represents a conic section in polar form. Identify the conic section, the position of the directrix, and the distance between the focus and the directrix.r = 
A. hyperbola, directrix perpendicular to the polar axis located 1 unit(s) left of the pole B. ellipse, directrix perpendicular to the polar axis located 1 unit(s) left of the pole C. hyperbola, directrix perpendicular to the polar axis located 1 unit(s) right of the pole D. ellipse, directrix perpendicular to the polar axis located 1 unit(s) right of the pole