Solve the problem.The amount of water (in gallons) in a leaky bathtub is given in the table below. Using a graphing utility, fit the data to a third degree polynomial (or a cubic). Then approximate the time at which there is maximum amount of water in the tub, and estimate the time when the water runs out of the tub. Express all your answers rounded to two decimal places.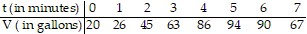
A. maximum amount of water after 5.31 minutes; water never runs out
B. maximum amount of water after 5.31 minutes; water runs out after 8.23 minutes
C. maximum amount of water after 8.23 minutes; water runs out after 19.73 minutes
D. maximum amount of water after 5.37 minutes; water runs out after 11.06 minutes
Answer: B
You might also like to view...
Fill in the blank with one of the words or phrases listed below. 
A(n) 
is a piece of a line with two endpoints.
A. transversal B. ray C. perimeter D. line segment
Set up the linear programming problem.A dietitian needs to purchase food for patients. She can purchase an ounce of chicken for $0.25 and an ounce of potatoes for $0.02. The dietician is bound by the following constraints.? Each ounce of chicken contains 13 grams of protein and 24 grams of carbohydrates.? Each ounce of potatoes contains 5 grams of protein and 35 grams of carbohydrates.? The minimum daily requirements for the patients under the dietitian's care are 45 grams of protein and 58 grams of carbohydrates. Let x = the number of ounces of chicken and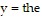 
number of ounces of potatoes purchased per patient. Write a system of inequalities that describes these
constraints.
A. 
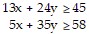
B. 
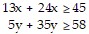
C. 
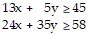
D. 
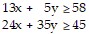
Graph the linear equation.x - y = -7
A.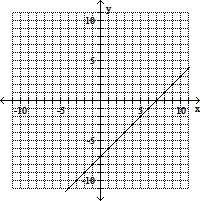 
B.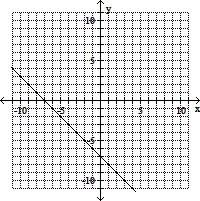 
C.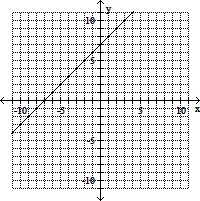 
D.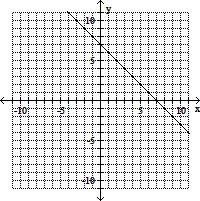 
Indicate whether the graph of the equation is a circle, an ellipse, a hyperbola, or a parabola. Then graph the conic section.3x2 = 147 + 3y2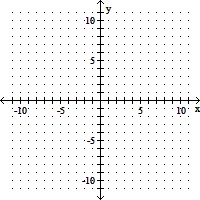
A. parabola
B. hyperbola
C. circle
D. ellipse