Solve the problem.The volume V of a square-based pyramid with base sides s and height h is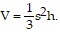 
If the height is half of the length of a base side, express the volume V as a function of s.
A. V(s) = 
s3h
B. V(s) = 
s2
C. V(s) = 
s3h
D. V(s) = 
s3
Answer: D
You might also like to view...
Solve the problem.V =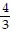 
?r3, where r is the radius, in centimeters. By approximately how much does the volume of a sphere increase when the radius is increased from 1.0 cm to 1.1 cm? (Use 3.14 for ?.)
A. 1.3 cm3 B. 1.5 cm3 C. 0.1 cm3 D. 1.1 cm3
Solve the problem.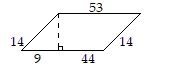
Find the area.
A. 44 
B. 742
C. 53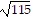 
D. 53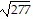 
Provide an appropriate response.Explain why the graph of a hyperbola does not satisfy the conditions for the graph of a function.
What will be an ideal response?
Approximate the coordinates of each turning point by graphing f(x) in the standard viewing rectangle. Round to the nearest hundredth, if necessary.f(x) = 0.1x4 - 0.55x3 + 0.3x2 - 0.15x - 2
A. (0, -2) and (3.75, -7.57) B. (-1.26, 0), (3.75, -7.57), and (5.12, 0) C. (3.75, -7.57) D. (-1.26, 0) and (5.12, 0)