Decide whether or not the points are the vertices of a right triangle.Consider the three points A = (3, -2), B = (1, 0), C = (-3, -4). Determine whether the triangle ABC is a right triangle. Explain your reasoning.
A. The side lengths of triangle ABC are d(A, B) = 2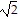
, d(A, C) = 2
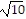, d(B, C) = 4.
[d(A, B)]2 + [d(B, C)]2 = (2
)2 + 42 = 8 + 16 = 24
[d(A, C)]2 = (2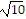
)2 = 40
Since [d(A, C)]2 ? [d(A, B)]2 + [d(B, C)]2 , triangle ABC is not a right triangle.
B. The side lengths of triangle ABC are d(A, B) = 2
, d(A, C) = 2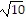
, d(B, C) = 4
.
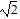[d(A, B)]2 + [d(B, C)]2 = (2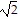
)2 + (4
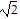)2 = 8 + 32 = 40
[d(A, C)]2 = (2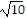
)2 = 40
Since [d(A, C)]2 = [d(A, B)]2 + [d(B, C)]2, triangle ABC is a right triangle.
C. The side lengths of triangle ABC are d(A, B) = 4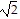
, d(A, C) = 2
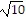, d(B, C) = 4.
[d(A, B)]2 + [d(B, C)]2 = (4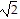
)2 + 42 = 32 + 16 = 48
[d(A, C)]2 = (2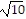
)2 = 40
Since [d(A, C)]2 ? [d(A, B)]2 + [d(B, C)]2, triangle ABC is not a right triangle.
D. The side lengths of triangle ABC are d(A, B) = 2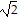
, d(A, C) = 4
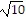, d(B, C) = 4
.
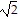[d(A, B)]2 + [d(B, C)]2 = (2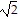
)2 + (4
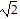)2 = 8 + 32 = 40
[d(A, C)]2 = (4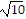
)2 = 160
Since [d(A, C)]2 ? [d(A, B)]2 + [d(B, C)]2, triangle ABC is not a right triangle.
Answer: B
You might also like to view...
Perform the indicated operations.5 - (8 - 9 ? 72)
A. -428 B. 438 C. 3966 D. -444
Find all values of x satisfying the given conditions.y = 
and y = 2
A. -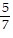 
, - 
B.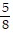 
, 
C. - 
, - 
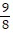
D. No solutions
The graph below shows the percentage of students enrolled in the College of Engineering at State University. Use the graph to answer the question.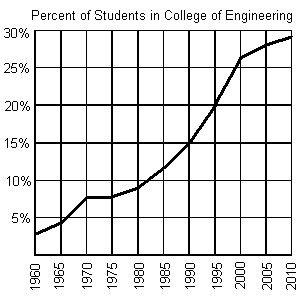
Find f(2005).
A. 30% B. 23% C. 28% D. 24.5%
Approximate using a calculator (set for radians). Round answers to two decimal places.
?
?
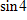
A. -0.65 B. -0.76 C. -0.99 D. 0.15 E. 0.35