Use the Principle of Mathematical Induction to show that the statement is true for all natural numbers n.6 + 12 + 18 + ... + 6n = 3n(n + 1)
What will be an ideal response?
First we show that the statement is true when n = 1.
For n = 1, we get 6 = 3(1)(1 + 1) = 6.
This is a true statement and Condition I is satisfied.
Next, we assume the statement holds for some k. That is,
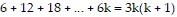 is true for some positive integer k.
is true for some positive integer k.
We need to show that the statement holds for k + 1. That is, we need to show that
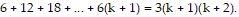
So we assume that 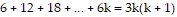 is true and add the next term,
is true and add the next term, 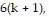 to both sides of the equation.
to both sides of the equation.
6 + 12 + 18 + ... + 6k + 6(k + 1) = 3k(k + 1) + 6(k + 1)
= (k + 1)(3k + 6)
= 3(k + 1)(k + 2)
Condition II is satisfied. As a result, the statement is true for all natural numbers n.
You might also like to view...
Match the correct function to the graph.
A. y = 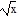
B. y = 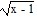
C. y = 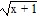
D. y = x - 1
Use the circle graph to solve the problem.The following figures give the distribution of land (in acres) for a county containing 94,000 acres. Identify each category on the circle graph.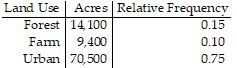
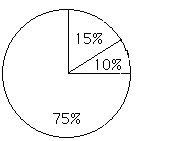
A. 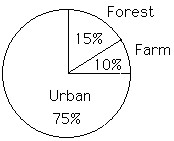
B. 
C. 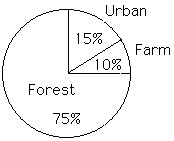
D. 
Perform the indicated operations and simplify the result. Leave the numerator and denominator in your answer in factored form.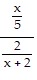
A. 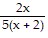
B. 10x(x + 2)
C. 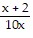
D. 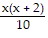
Solve the problem.One pump can drain a pool in 10 minutes. When a second pump is also used, the pool only takes 9 minutes to drain. How long would it take the second pump to drain the pool if it were the only pump in use?
A. 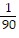 minute
minute
B. 4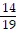 minutes
minutes
C. 90 minutes
D. 89 minutes