Use the Principle of Mathematical Induction to show that the statement is true for all natural numbers n.Show that the formula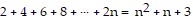 
obeys Condition II of the Principle of Mathematical Induction. That is, show that if the formula is true for some natural number k, it is also true for the next natural number 
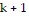. Then show that the formula is false for 
.
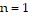What will be an ideal response?
Assume the statement is true for some natural number k. Then
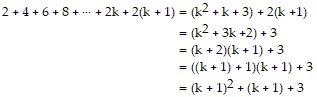
So the statement is true for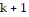 
.
However, when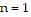 
, the left side of the statement is 
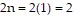, and the right side of the statement is 
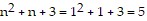, so the formula is false for 
.
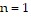Mathematics
You might also like to view...
Evaluate the improper integral.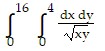
A. 16 B. 48 C. 32 D. 8
Mathematics
Evaluate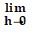 
for the given x0 and function f.f(x) = 
+ 8 for x0 = 6
A. 
B. 
C. Does not exist
D. 
Mathematics
Evaluate the integral by using a substitution prior to integration by parts.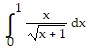
A. -1.33 B. -2.27 C. -0.94 D. 0.39
Mathematics
Use multiplication to check the answer. If an answer is incorrect, find the correct answer.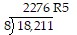
A. Incorrect; should be 2281 R5 B. Correct C. Incorrect; should be 2276 R3 D. Incorrect; should be 2276 R4
Mathematics