Solve.The area of a rectangle with sides of length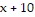 
and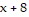 
is given by the function 
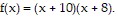The area of a smaller rectangle inside of the larger rectangle is given by the function 
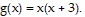Find a function h that gives the area of the region inside the larger rectangle and outside the smaller rectangle.
A. h(x) = x4 + 21x3 + 42x2 + 80x
B. h(x) =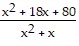 
C. h(x) = 15x + 80
D. h(x) = 2x2+ 21x + 80
Answer: C
You might also like to view...
Solve the problem using two linear equations in two variables and Cramer's rule.The perimeter of a rectangle is 24 units. If the width is doubled and the length is tripled, the perimeter is 60 units. Determine the original width and length.
A. width = 10 units, length = 20 units B. width = 8 units, length = 12 units C. width = 6 units, length = 6 units D. width = 12 units, length = 12 units
Find the quotient.-264 ÷ (33)
A. -18
B. 8
C. - 
D. -8
Is it possible using only a straightedge and a compass, to reproduce a circle with a radius congruent to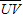 
?
?
?
?
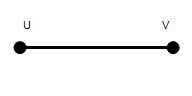
A. No B. Yes
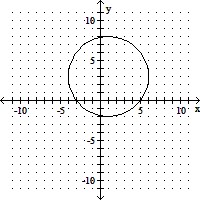
Write the equation of the circle in standard form. Find the center and radius. Then sketch the graph.x2 + y2 + 2x + 6y - 15 = 0
A. (x + 1)2 + (y + 3)2 = 25
(h, k) = (-1, -3), r = 5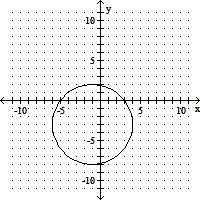
B. (x - 1)2 + (y + 3)2 = 25
(h, k) = (1, -3), r = 5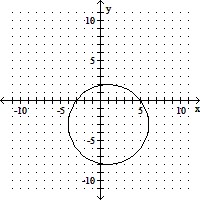
C. (x + 1)2 + (y - 3)2 = 25
(h, k) = (-1, 3), r = 5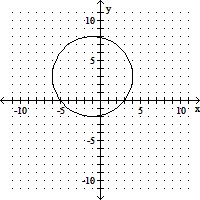
D. (x - 1)2 + (y - 3)2 = 25
(h, k) = (1, 3), r = 5