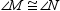Provide missing statements and missing reasons for the proof of the theorem,“If two sides of a triangle are congruent, then the angles opposite those sides arealso congruent.”Given: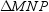 
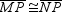
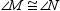
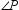
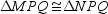
with 
Prove: 
S1. R1.S2. Draw the angle bisector for 
R2. Every angle has exactly one angle-bisector.S3. 
R3.S4. R4.
What will be an ideal response?
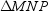with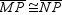 
R1. Given
R3. The bisector of the vertex angle of an isosceles triangle separates the triangle into
two congruent triangles.
S4. 
R4. CPCTC
You might also like to view...
Solve the problem.Find the center of mass of the region common to the spheres ? = 2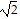
cos ? and ? = 2.
A. (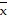
, 
, 
) = 
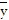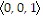
B. (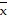
, 
, 
) = 
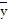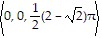
C. (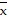
, 
, 
) = 
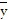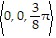
D. (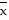
, 
, 
) = 
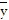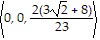
Using Green's Theorem, compute the counterclockwise circulation of F around the closed curve C.F = (x - y)i + (x + y)j; C is the triangle with vertices at (0, 0), (7, 0), and (0, 6)
A. 42 B. 84 C. 0 D. 252
Find the indicated root of the given equation by using Newton's method.2x4 - 3x2 - 7x + 1 = 0 (between 0 and 1)
A. 0.1351270 B. 0.1351020 C. 0.1351239 D. 0.1351097
Determine whether the given geometric series is convergent or divergent, and find the sum if it is convergent.1 +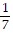 
+ 
+ 
+ ...
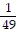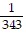A. Convergent; S = 1.75 B. Divergent C. Convergent; S = 1.3125 D. Convergent; S = 1.1667