Use mathematical induction to prove that the statement is true for every positive integer n.9n > 1
What will be an ideal response?
Answers will vary. One possible proof follows.
a). Let n = 1. Then, 91 = 9 > 1, so the statement is true for n = 1.
b). Assume the statement is true for n = k:
9k > 1
Multiply both sides by 9:
9 ? 9k = 9k + 1 > 1 ? 9 = 9 or 9k + 1 > 9. Also, 9 > 1, so 9k + 1> 1.
Since the statement is true for n = k + 1 as long as it is true for n = k, and since the statement is true for n = 1, then it is true for all natural numbers n.
You might also like to view...
Calculate the flow in the field F along the path C.F = 5i + 8j + 7k; C is the curve r(t) = 8 cos 8ti + 8 sin 8tj + 3tk , 0 ? t ?  ?
?
A. 208 + 126?
B.  ?
?
C. 48 + 126?
D. 80 + 126?
Solve the problem.Find the point on the line 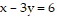 that is closest to the origin.
that is closest to the origin.
A. 
B. 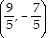
C. 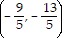
D. 
Find the exact value of cos(x-y) given that sec x = 3 / 2, csc y = 3, and x and y are in quadrant 1.
What will be an ideal response?
Add: (2+7j)+(-3+4j)
What will be an ideal response?