?V is the vertex angle of isosceles triangle ?RVT. Prove that if VS is the median to RT, then bisects ?RVT.
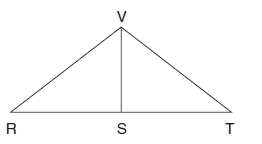
(Outline) Since ?RVT is isosceles with ?V the vertex angle, RV ?VT. Then, in ?RVT,?R ? T since they are opposite congruent sides. VS is the meridian to RT ? RS? ST. Then ?RVS ? ?TVS by S.A.S. By C.P., ?RVS ? ?TVS. Thus VS bisects ?RVT.
You might also like to view...
Solve the problem.If the Hamilton Method is used to apportion legislative seats to two original states and a new state with the populations given in the table (in thousands), then one of the states loses a seat to another if the original number of seats being apportioned is 48.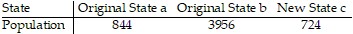 
Which state loses a seat to which state, and does the New States paradox occur?
A. a loses a seat to b, no B. b loses a seat to a, yes C. b loses a seat to a, no D. a loses a seat to b, yes
Provide an appropriate response.Find the quotient.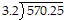 
A. 178 B. 178 R65 C. 178.203125 D. 5.61157387
Solve the compound inequality. Express the solution using interval notation. Graph the solution set.x ? 2 or x ? 5
A. (-?, 2] ? [5, ?)
B. [-5, -2]
C. (-2, 5)
D. (2, 5)
Find an expression, in factored form, for the area of the shaded region.
A. (x + 4)(x + 8) B. (x - 3)(x - 9) C. (x + 3)(x + 9) D. (x + 5)(x + 7)