Find the domain and range of the relation.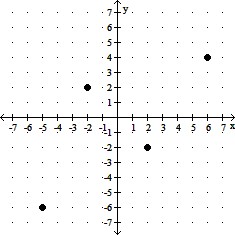
A. domain: {-6, -2, 2, 4}, range: {-5, -2, 2, 6}
B. domain: (-?, ?), range: (-?, ?)
C. domain: (-?, ?), range: {-6, -2, 2, 4}
D. domain: {-5, -2, 2, 6}, range: {-6, -2, 2, 4}
Answer: D
You might also like to view...
The body surface area B, in square meters, of a man who is 180 centimeters tall can be estimated from his weight w, in kilograms. The relationship is
.
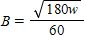
Wha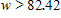t weight range results in a b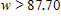ody surfac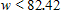e area of more than 2.03 meters? Round 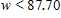your answer to two decimal places.
?
A. 
kilograms
B. 
kilograms
C. 
kilograms
D. 
kilograms
Simplify the expression.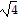
A. 16
B.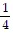 
C. 2
D. not a real number
Solve the system of equations.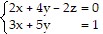
A. x = -2 - 7z, and y = -3z -1, where z is any real number
or {(x, y, z) |x = -2 - 7z, and y = -3z -1, where z is any real number}
B. x = 2 + 7z, and y = -3z - 1, where z is any real number
or {(x, y, z) |x = 2 + 7z, and y = -3z - 1, where z is any real number}
C. x = 2 - 5z, and y = 3z - 1, where z is any real number
or {(x, y, z) |x = 2 - 5z, and y = 3z - 1, where z is any real number}
D. x = 1 - 5z, and y = 3z -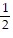 
, where z is any real number
or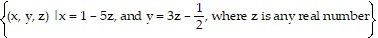 
An objective function and a system of linear inequalities representing constraints are given. Graph the system of inequalities representing the constraints. Find the value of the objective function at each corner of the graphed region. Use these values to determine the maximum value of the objective function and the values of x and y for which the maximum occurs.Objective Functionz = 10x - 23yConstraints0 ? x ? 5 0 ? y ? 8 4x + 5y ? 30 4x + 3y ? 20
A. Maximum: -102.5; at (1.25, 5) B. Maximum: 0; at (0, 0) C. Maximum: -138; at (0, 6) D. Maximum: 50; at (5, 0)