Two curves are said to be orthogonal if their tangent lines are perpendicular at each point of intersection of the curves. Show that the curves of the given equations are orthogonal.
The curves intersect at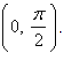 
For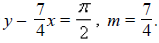 
For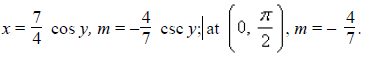 
You might also like to view...
Simplify the expression. [-4m + (-10m - 6)] - [(10m + (1 - 6m)) + 4m]
A. -14m + 7 B. -14m - 5 C. -22m - 7 D. -6m - 5
Find at least three nonzero terms [including a0, at least two cosine terms (if they are not all zero) and at least two sine terms (if they are not all zero)] of the Fourier series for the given function.f(x) = x + ? -? ? x < ?
A. f(x) = ? + sin x -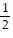 
sin 2x + 
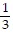sin 3x - . . .
B. f(x) = ? + 2 sin x - sin 2x + . . .
C. f(x) = 2 sin x - sin 2x + 
sin 3x - . . .
D. f(x) = ? + sin x - 
sin 2x + . . .
Find an equation of the sphere that passes through the point (7,-4,9) and has center (-4,5,-5).
What will be an ideal response?
Write the equation of the line in slope-intercept form.m = -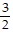 
, y-intercept (0, 8)
A. y = -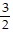 
x + 8
B. y = - 
x - 8
C. y = 
x - 8
D. y = 
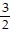x + 8