Solve the problem.Ken is 6 feet tall and is walking away from a streetlight. The streetlight has its light bulb 14 feet above the ground, and Ken is walking at the rate of 4.2 feet per second. Find a function, d(t), which gives the distance Ken is from the streetlight in terms of time. Find a function,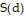 
, which gives the length of Ken's shadow in terms of d. Then find 
.
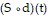A. (S ? d)(t) = 3.99t
B. (S ? d)(t) = 3.15t
C. (S ? d)(t) = 2.31t
D. (S ? d)(t) = 7.1t
Answer: B
You might also like to view...
Provide an appropriate response.Use the trapezoidal rule with n = 3 to estimate the value of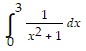 
Fill in the blank(s) with the appropriate word(s).
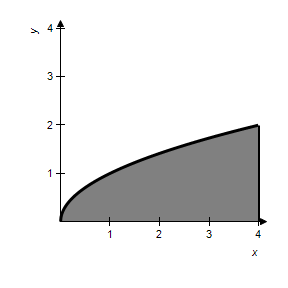
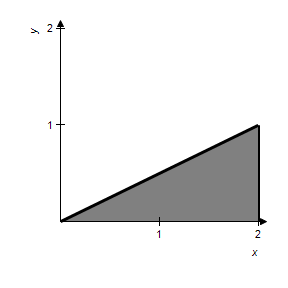
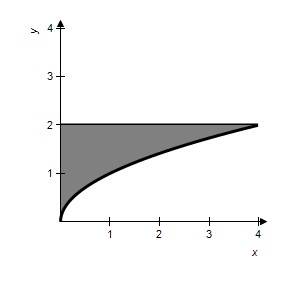
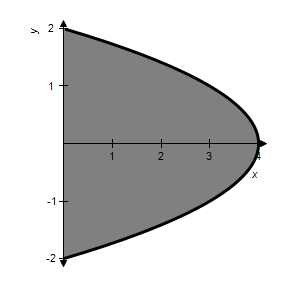
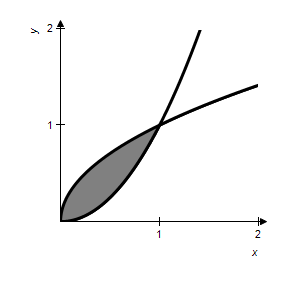
Sketch the region R whose area is given by the following double integral.
?
?
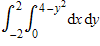
A. ??
B. ?
C. ?
?
D. ?
E. ?
?
Solve the problem.A police helicopter is monitoring the speed of two cars on a straight road. The helicopter is at an altitude of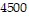 
feet directly above the road. At one instant, the angle of elevation from the first car to the helicopter is 
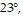and the angle of elevation from the second car to the helicopter is 
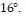How far apart are the two cars to the nearest foot?
A. 620 ft B. 4809 ft C. 207 ft D. 5092 ft
Find the maximum value of the objective function and where it occurs, subject to the constraints: ? Objective function: ? z = 12x + 24y ? Constraints: ? x ? 0 y ? 0 x + 4y ? 20 x + y ? 18 ?2x + 2y ? 21 ?
A. Maximum at (0, 5): 120
B. Maximum at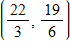 
: 164
C. No maximum
D. Maximum at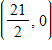 
: 126
E. Maximum at (0, 0): 0