Solve the linear programming problem.The Fiedler family has up to $130,000 to invest. They decide that they want to have at least $40,000 invested in stable bonds yielding 5.5% and that no more than $60,000 should be invested in more volatile bonds yielding 11%. How much should they invest in each type of bond to maximize income if the amount in the stable bond should not exceed the amount in the more volatile bond? What is the maximum income?
What will be an ideal response?
$60,000 in the stable bonds and $60,000 in the volatile bonds; maximum income $9900
You might also like to view...
Convert as indicated. If necessary, round to the nearest tenth of a degree.91°F to degrees Celsius
A. 32.8°C B. 106.2°C C. 82.6°C D. 195.8°C
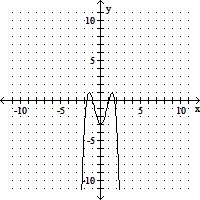
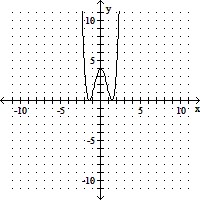
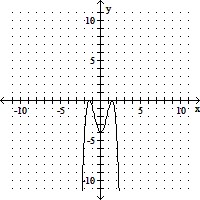
Sketch the graph and show all local extrema and inflection points.f(x) = -x4 + 4x2 - 4
A. Local maxima: (-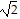
, 0), (
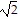, 0)
Local minimum: (0, -4)
No inflection points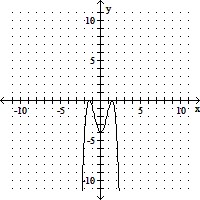
B. Local maxima: (-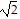
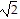, 0), (
, 0)
Inflection points: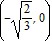 
, 
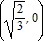
C. Local minima: (-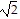
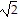, 0), (
, 0)
Local maximum: (0, 4)
Inflection point: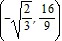 
, 
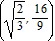
D. Local maxima: (-
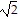, 0), (
, 0)
Local minimum: (0, -4)
Inflection points: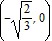 
, 
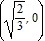
Find the indicated derivative.Find y(4) if y = -5 cos x.
A. y(4) = -5 cos x B. y(4) = -5 sin x C. y(4) = 5 sin x D. y(4) = 5 cos x
Simplify.Write 64,776 in words.
A. sixty thousand, seven hundred seventy-six B. sixty-four thousand, seven hundred seventy-six C. sixty-four thousand, seventy-seven hundred, six D. six thousand, seven hundred seventy-six